Dimensión de una matriz Þ número de filas x numero de columnas. Dimensión mxn
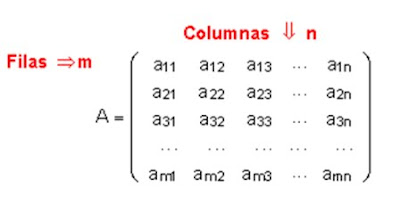 ejemplo:
ejemplo: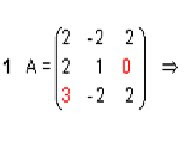 Dimensión 3x3, m=3 filas y n=3 columnas
Dimensión 3x3, m=3 filas y n=3 columnasTIPOS DE MATRICES:
- Rectangulares: m es diferente a n, dimensión m x n
- Cuadradas: m es igual a n, dimensión n x n, se llaman de orden n.
matriz rectangular

matriz fila : tiene una sola fila, dimensión 1 x n. B = (2 5 -3 0) dimensión 1x4
matriz columna: tiene una sola columna, dimensión m x 1
OPERACIONES CON MATRICES
Trasposición
La matriz traspuesta, AT, de la matriz A es la matriz que se obtiene cambiando las filas por las columnas (o viceversa) en la matriz A.
Sea A una matiz m×n y B = AT, entonces B es la
matriz n×m con bij = aji.
ejemploSuma y Resta
Sea A y B matrices con las mismas dimensiones,
suma, A+B, se obtiene sumando entradas correspondientes. En símbolos,
(A+B)ij = Aij + Bij.
resta, A - B, obtiene restando entradas correspondientes. En símbolos, (A-B)ij = Aij - Bij.

Producto escalar
Sea A una matriz y c un número (llamado un escalar en este contexto),
Definimos el producto escalar por la matriz, cA, como la matriz que se obtiene multiplicando cada entrada de A por c. En símbolos, (cA)ij = c(Aij).
Producto
Sea A una matriz con dimensiones m×n y B una matriz con dimensiones n×p, entonces el producto AB está definido, y tiene dimenciones m×p.
La entrada (AB)ij se obtiene por multiplicar reglón i de A por columna j de B, hecho por multiplicar sus entradas correspondientes y sumar las resultados.
LA MATRIZ UNIDAD DE ORDEN NXN
La matriz unidad de orden n×n es la matriz I de orden n×n en la cual todas las entradas son cero excepto los de la diagonal principal, que son 1.
En símbolos:
- Iij = 1 si i = j y Iij = 0 si i ≠ j.
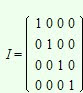
Una matriz cero es una matriz O en la cual todas las entradas son
Sea A una matriz cuadrada, es decir, una matriz cuyo número de reglones es igual a su número de filas, entonces es posible a veces despejar a X en una ecuación matriz AX = B por "dividir por A." Precisamente, una matriz cuadrada A puede tener una inversa, que se escribe como A-1, con la propiedad
- AA-1 = A-1A = I.
En el caso de A invertible, podemos despejar a X en la ecuación
- AX = B
- X = A-1 B.
ejemplo:
El sistema de ecuaciones
tiene la solucion

Inversa de una matriz 2×2
La matriz 2×2
ejemplo:
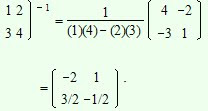
Las operaciones de adición
multiplicación escalar, multiplicación entre matrices se cumplen las siguientes reglas:
| A+(B+C) = (A+B)+C | Regla asociativa de adición |
| A+B = B+A | Regla conmutativa de adición |
| A+O = O+A = A | Regla unidad de adición |
| A+( - A) = O = ( - A)+A | Regla inversa de adición |
| c(A+B) = cA+cB | Regla distributiva |
| (c+d)A = cA+dA | Regla distributiva |
| 1A = A | Unidad escalar |
| 0A = O | Cero escalar |
| A(BC) = (AB)C | Regla asociativa de multiplicación |
| AI = IA = A | Regla unidad de multiplicación |
| A(B+C) = AB + AC | Regla distributiva |
| (A+B)C = AC + BC | Regla distributiva |
| OA = AO = O | Multiplicación por matriz cero |
| (A+B)T = AT + BT | Trasposición de una suma |
| (cA)T = c(AT) | Trasposición de un producto escalar |
| (AB)T = BTAT | Trasposición de un producto matriz |
La única regla que está notablemente ausente es la de conmutatividad del producto entre matrices. El producto entre matrices no es conmutativo: AB no es igual a BA en general.
APLICACION ECONOMICA
modelos económicos de insumo-producto
Una matriz insumo-producto para una economía da, en su ja columna, las cantidades (en dólares o otra moneda apropiada) del productos de cada sector usado como insumo por sector j (en un año o otra apropiada unidad de tiempo). Da también la producción total de cada sector de la economía durante un año (llamada el vector producción cuando está escrito como una columna).
La matriz tecnología es la matriz que se obtiene dividiendo cada columna por la producción total del sector correspondiente. Su ija entrada , el ijo coeficiente tecnología, da el insumo de sector i para producir una unidad de producto del sector j. Un vector demanda es un vector columna que expresa la demanda total desde fuera la economía de los productos de cada sector. Sea A la matriz tecnología, X el vector producción, y D el vector demanda, entonces
- (I - A)X = D,
- X = (I - A)-1D.
Estas mismas ecuaciones son válidas si D es un vector que representa cambio de demanda, y X es un vector que representa cambio de producción. Las entradas en una columna de (I - A)-1 representan el cambio en producción de cada sector necesario para satisfacer una unidad de cambio de demanda en el sector que corresponde a aquella columna, tomando en cuenta todos los efectos directos y indirectos
estos son algunas paginas que pueden consultar para obtener mas informacion sobre matrices.
www.vitutor.com/algebra/matrices/operaciones.html
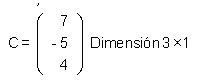




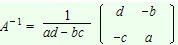


Muy buen ejercicio, felicitaciones.
ResponderEliminarSaludos, Otto